非均质碳酸盐岩储层不同储层岩石分类方法的胶结系数预测

胶结指数或胶结因子是阿尔奇方程中最重要的因素之一，为了准确确定储层的相关岩石物性特征，必须对其进行精确估计。该系数的不准确估计将导致岩石物性分析的不准确和含水饱和度的不准确确定，而含水饱和度对油气藏经济预测具有重要意义。一种替代胶结系数精确估计的方法是根据常见的岩石物理性质(如渗透率)对岩石进行分类。本研究旨在研究不同岩石类型的胶结系数，并根据不同的岩石分类方法，最终提供一个合适的胶结系数估算模型。本文首先采用常规岩石分类方法(如电流区指标(current zone indicator, CZI)、流动区指标(flow zone indicator, FZI)、渗透率和电效率)估算胶结系数。然后，利用这些方法对Regnet等人(J Geophys Res Solid Earth 120:790-811, 2015)的数据进行分析，以找到最佳的岩石分类方法。分析数据表明，只有电效率法才能准确地将岩石划分为不同的类别，因为电效率法对岩石进行分类，得到了较高的确定系数(即0.9828和0.9725)，将岩石划分为不同的类别。渗透率法、FZI法和CZI法的确定系数分别为0.805、0.809和0.7568。由于这一结果和分类数据的高散射性，可以得出结论，这三种方法对数据的岩石分类不够精确。除了上述已有的方法外，本文还提出了一种基于扭曲系数或因子的岩石分类新方法。由于新方法对数据结果的散射小、分组清晰，并且在分类中获得了较高的决定系数(分别为0.9996、0.9986和0.9951)，因此证明了新方法的准确性。

非常规油气资源蕴藏量巨大，但其地质特征普遍存在，制约了油气在储层中的流动。这些资源的岩石物理性质也与常规储层不同，其复杂的岩性给准确评估地层的孔隙度、渗透率和含水饱和度带来了挑战(Muther et al. 2022)。含水饱和度是预测油气藏发育的重要参数(Rezaee et al. 2007;al - gathe et al. 2009)。

1942年，Archie首次尝试利用测井数据估算含水饱和度。该方法需要在实验室测量胶结系数，但由于非常规油藏岩性复杂，胶结系数沿井筒深度变化很大，假设胶结系数为恒定值会导致含水饱和度的测定出现误差(Heydari Gholanlo等，2018)。此外，获得胶结系数值的实验室测量既昂贵又耗时(Mahmoodpour et al. 2021)。

为了建立胶结因子的适当关系，许多作者提出了各种各样的方程。然而，在大多数这些方程中，胶结系数被假定为常数。假设胶结系数为恒定值将导致不精确的岩石物理评价。为了消除不准确性，不应假设胶结系数恒定(Soleymanzadeh et al. 2018;Ara et al. 2001;Hasanigiv and Rahimi 2008;Focke et al. 1987)。

由于碳酸盐岩储层的复杂性，特别是这些储层的非均质性，以及各种岩石类型的存在，为了确定精确的胶结系数，对于所讨论的每种岩石，需要不同的方程。这有助于形成新的储层岩石分类和岩石类型方法(Focke et al. 1987)。

本文采用Regnet et al.(2015)的数据，采用不同的方法(如CZI、FZI、渗透率和电效率)进行分析，并提出了最准确的岩石分类方法。除了现有的岩石分类方法外，还提出了一种新的岩石分类方法。提出了一种基于扭曲系数或扭曲因子的岩石电性分类方法，提高了胶结系数的估计，从而获得了更精确的含水饱和度。

Archie(1942)是第一个发现地层电阻率系数(F)和孔隙度(φ)之间关系的人，他在对数交叉图上对它们进行了说明。然后，他以以下形式提出了两者之间的相关性:

（1）

他发现，在式(1)中，地层电阻率系数图与孔隙度的对数斜率为胶结系数，而胶结系数是岩石物理学中的关键参数。

后来，Winsauer et al.(1952)在Archie的方程中增加了另一个参数，称为扭曲系数(a):

（2）

式(2)称为Archie-Winsauer相关。

Humble’s相关性是估算地层电阻率系数最常用的相关性之一，表示形式如下:

（3）

Humble的相关性由Winsauer et al.(1952)发展而来。

随后，Carothers使用793个砂岩样本(Mabrouk et al. 2015)得到式(4):

（4）

此后，Timur et al.(1972)在分析了1800个砂岩样本后提出了以下相关性(Tiab et al. 2015):

（5）

Tixier et al.(1965)在预测胶结因子时接近了Humble-like相关性:

（6）

在非裂缝性碳酸盐岩储层中，基于孔隙度估算胶结系数值，可采用Shell对比法(Kadhim et al. 2013)。

(7）

Borai(1987)通过分析64个碳酸盐样品预测胶结因子，提出了以下相关性:

（8)

Gomez是第一个获得相关性来估计每个表面积的胶结系数和扭曲系数的学者(Rivero et al. 1978;Watfa et al. 1987):

（9）

Assadollahi等人(2008)提出了以下相关性，可用于估计伊朗碳酸盐岩储层的胶结系数:

(10)

因此，不同的作者提出了许多相关性来估计胶结系数，但只有很少的相关性能得出准确的胶结系数值。许多岩石样品的岩石物理分析和地质研究表明，根据其相互特征(即渗透率、孔隙类型、FZI和电效率)对这些样品进行分类将得到更好、更准确的胶结系数值(Rezaee et al. 2007;Soleymanzadeh et al. 2018;Soleymanzadeh et al. 2021)。

为了更准确地估计孔隙度与地层电阻率因子之间的相关性，提出了不同的分类方法。

Hasanigiv和Rahimi(2008)对伊朗西南部Asmari、Ilam和Sarvak组的155个岩心样本进行了研究。根据岩石类型和孔隙类型，他们将样品分为6类，如表1所示。

Focke和Munn(1987)在对非均质碳酸盐岩储层进行研究后，认识到含水饱和度估算不确定的主要原因是胶结系数。之后，他们根据渗透率值对石灰石样品进行分类，并在对数交叉图上展示地层电阻率系数与孔隙度的关系。最后，他们为每一类渗透率提出了如下方程:

(11) (12) (13) (14)

分析结果表明，尽管已分别对各类进行了说明，但并不能很好地拟合每一类。这可能是因为渗透率与地层电阻率因子之间的关系较弱(Rezaee et al. 2007)。

一般来说，孔隙度和渗透率之间的关系很弱。为了更好地找到孔隙度和渗透率之间的关系，并解释水力流量单位(HFU)， Amaefule et al.(1993)提出了如下公式:

(15)

FZI、k、分别为流区指标(μm)、渗透率(mD)、孔隙度(分数)，为基质体积比(PMR)，计算公式为:

（16）

这个方程显示了孔隙或空隙空间及其几何分布之间的关系。

Rezaee et al.(2007)根据公式(15)得到的FZI值对储层样品进行分类，然后通过FZI测井将其划分为不同的hfu。分隔hfu的FZI类是:

图1显示了地层电阻率系数与孔隙度的关系。从图中可以看出，每个HFU的数据是分散的，这意味着这种方法不能很好地对数据进行分类。这意味着液压和电路径不相同，液压扭曲比电扭曲大得多(Rezaee et al. 2007)。

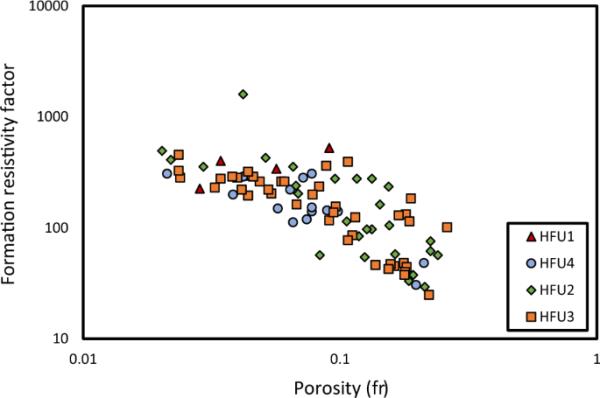
在对数交叉图上孔隙度与地层电阻率因子的关系。根据样本的FZIs，将样本分为四类HFU (Rezaee et al.， 2007)。

在地层电阻率对孔隙度的对数交叉图中，数据可能存在较高的散射率。这可能导致R2(决定系数)的值较小，因此，它将导致估计m和a值的高误差(Rezaee et al. 2007)。

Amaeful et al.(1993)结合柱状管内流动的Poiseuille定律、多孔介质中流体流动的Darcy定律和Kozney-Carmen模型定义了储层质量指数(RQI):

(17)

RQI值越大，说明储层质量越好。

然而，地层电阻率系数与渗透率之间并没有普遍的关系，但许多作者报道了它们之间的反比关系(如Wong et al. 1984;Kostek et al. 1992;Nettelblad et al. 1995;Celzard et al. 2002)。

电半径指示器(ERI)可用下式定义:

(18)

与RQI给出水力半径的平均值不同，ERI是无量纲的，并且只比较样品的电半径。由式(18)可知，在孔隙度一定的情况下，地层电阻率系数降低会增加ERI，反之亦然。

Rezaee et al.(2007)比较了92个样本的RQI和ERI值(图2)。该图中RQI和ERI的不一致性可以表明液压路径和电气路径的差异。

92个样本RQI和ERI值的比较(Rezaee et al.， 2007)

ERI是每个样品的电路径符号。为了分离具有相似电流量的样品，ERI应划分为孔隙体积，或者更准确地说，划分为孔隙体积与基质的比值:

(19)

其中CZI为当前区域指示器。这个方程定义了空隙体积和电流特性之间的关系。该方程可以划分电流值相近的样品，因此称为电流区指示器或CZI (Rezaee et al. 2007)。CZI是一个可以用来分离m和a值非常相似的样品的因子，其中地层电阻率因子的变化只受孔隙度的影响。对于特定CZI范围内的每个样品，提出了具有相似电流量的单元。很明显，在与电性相似的储层距离相等的情况下，它表现出接近的czi。这种具有相似电流特性的范围称为电流单元(EFU)。Rezaee et al.(2007)使用四类CZI对四种efu进行分类:

图3显示了四种CZI类型地层电阻率系数与孔隙度的对数交叉图。

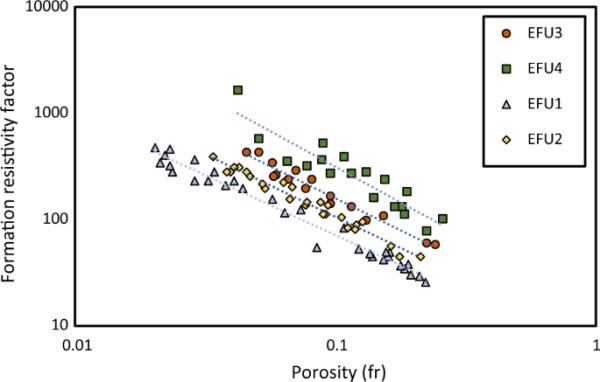
在对数交叉图上孔隙度与地层电阻率因子的关系。根据CZI值将样本分为四种efu (Rezaee et al.， 2007)。

表2给出了各EFU的CZI分类、最佳功率方程、孔隙度与地层电阻率系数之间的m、a和R2。使用这种方法，R2显著增加，这将有助于获得更准确的m和a值(Rezaee et al. 2007)。

一些作者认为扭度系数和胶结系数之间存在直线效应，即扭度系数越高，岩样的电流传导路径越难。Rezaee et al.(2007)认为这两个参数不一定是相互关联的。这意味着岩石试样的弯曲系数会发生变化，但胶结系数的值不会发生变化，反之亦然。在Herric和Kennedy(1994)提出的模型中，直管的电导率Cs为CwVw，其中Cw为填充管道的水的电导率，Vw为管道占用的孔隙体积。Vw可以通过表达式Sw来估计。因此，可以说:

（20）

其中E为比例系数，对于清洁岩石的总导电性，可得到以下公式:

（21)

E表示具有最大电流的岩样通过直管时的电流效率。对于水完全饱和的岩石，使用以下相关性来估计电效率:

(22)

岩石的电效率与水量无关，只受电流分布不均匀的影响。

Soleymanzadeh等人(2021)利用这一概念为岩石分类提供了一个新的参数，称为电效率。似乎电效率是孔隙度与地层电阻率因子的适当分类，从而产生不同的类别。对方程两边取对数，改写式(22)，得到:

(23)

这表明，如果我们在对数尺度上绘制孔隙度与地层电阻率因子的关系，对于所有具有相同电效率的岩石样品，我们得到一条斜率为-1的直线，因此，我们得到了不同的电性岩石类型。在这个对数交叉图上存在不同的平行线意味着岩石样品的不同电性类别。每条直线的截距是的倒数。因此，截距值越高，该类电性岩石的电效率越低，这就形成了一类电性岩石的胶结系数与孔隙度之间的新方程(Soleymanzadeh et al. 2021)。

(24)

合并Eq.(22)和(24)，得到Eq. (25):

(25)

在这种相关性中，对于每个ERI，存在具有相似电效率的类似样品。胶结系数与电效率倒数的结果是一条斜率为，截距为1的直线(Soleymanzadeh et al. 2021)。

摘要
介绍
理论背景
方法
结果与讨论
结论
缩写
参考文献

作者信息
道德声明



搜索
导航

＃＃＃＃＃

在本研究中，对Regnet等人(2015)报道的巴黎盆地东部石灰岩中的112个岩石样本进行了分析。这个数据集包括m, F, a, k。后来因为信息不足，删除了18个数据。图4显示了数据中孔隙度和渗透率值的范围。

Regnet et al.(2015)报告的94份碳酸盐岩样品孔隙度(左)和渗透率(右)

表3显示了每个参数的区间，包括m、F和k，说明该数据集涵盖的数据范围很广。

为了找到最佳的岩石分类方法并估计出准确的胶结系数值，在数据集上应用了不同的岩石分类方法。图5显示了研究的方法学流程图。首先，采用Focke和Munn(1987)提出的方法对数据进行分析，该方法根据渗透率值将数据分成几组。然后，将Amaefule等人(1993)提出的方法应用于根据FZI类导致数据中有不同组的数据。然后，根据他们的CZI类对数据进行分组。最终，Soleymanzadeh等人(2021)提出的方法被应用于数据，根据数据的电效率产生不同的分组。本研究在对Regnet et al.(2015)的数据集进行这四种方法的应用之后，又提出了一种基于数据扭曲系数分类的新方法，并对数据进行了应用，最终提出了岩石分类的最佳方法。

研究的方法学流程图

在本节中，上述五种方法已应用于Regnet et al.(2015)报告的数据。

根据渗透率值对数据进行分类(即Focke和Munn(1987)提出的方法)，将数据分为3个不同的渗透率区间(0.01 < k < 0.05, 0.05 < k < 0.5, 0.5 < k < 0.1)，然后对这3组进行F-对数图。图6显示了这些组按渗透率值分类的F对数图。

不同岩石组的F-对数图，根据它们的渗透率范围值进行分类

图7描绘了渗透率值3个区间的m-图。从图中可以看出，胶结系数数据与孔隙度值的关系非常分散。

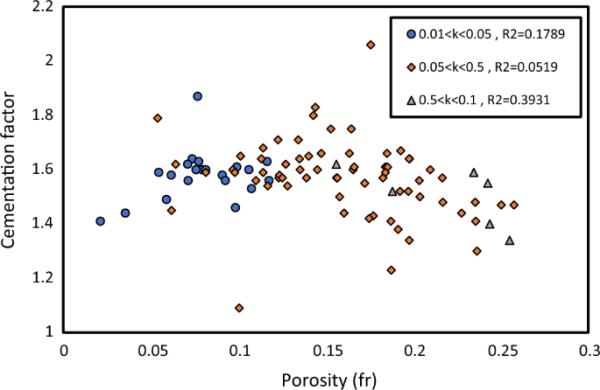
M -图对不同组的岩石进行了分类，并根据它们的渗透率范围值进行了分类

表4显示了从图6中提取的三个渗透率层的F-方程、a、R2和m。

表5显示了从图7中提取的三个渗透率组的m-方程和R2。

从图6和表4可以看出，虽然得到的数据散射程度较低，R2值较高(分别为0.8583、0.805和0.9569)，但由于没有将数据分门别类，渗透率并不能作为岩石分类的准确方法。其原因是渗透率作为主要的岩石物性与水力特性有关;因此，它不能说明石灰石的良好电性分类。

在本节中，为了按照FZI对数据进行分组，首先使用Eq.(15)估算每个岩石样本的FZI。

图8展示了log FZI的概率图。这个地块有不同的点，形成不同坡度的折线。每条线描绘了一组岩石，在RQI- plot上斜率为-1。在说明了概率图之后，每条线将被视为F-对数图的一个间隔。然后，如果每个基团都属于不同的基团，则表明FZI在分离液压路径的同时也会分离电路径。然而，这种情况在碳酸盐岩中并不常见，并且通过电路径的流体具有不同的特征，因此不能根据碳酸盐岩的fz进行分类。图9表示从图8的概率图中得到的每个对数FZI区间的F-对数图。

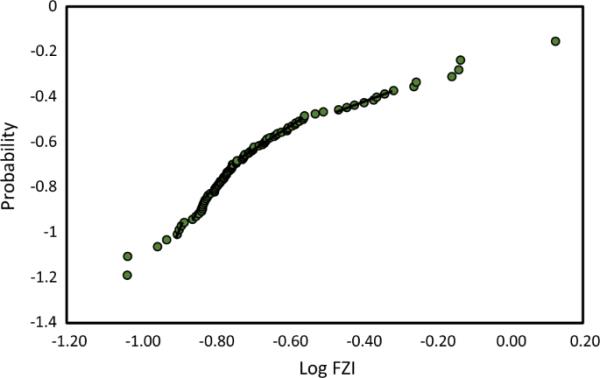
FZI数据的概率图

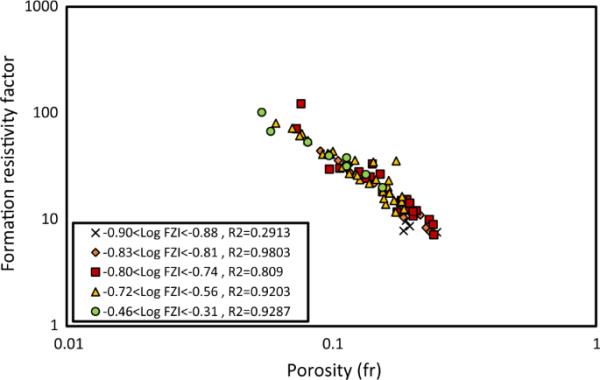
每组岩石的F-对数图，按其FZI范围值进行分类

如图9所示，各FZI组的数据散射程度较高。此外，第一组的R2值较低，为0.2913，在FZI数据中FZI范围最低。从这张图中可以看出，没有一个数据属于不同的组。其原因是碳酸盐岩的复杂性，而且FZI基于渗透率，这两者都描述了流体的水力行为。因此，它不能准确地用于电岩石分型。水力路径与电路径不同，因此FZI不是石灰石电分类的合适方法。

为了根据CZI值对岩石进行分类，首先，我们使用公式(19)计算了每个岩石样本的CZI。然后，将数据分为3个CZI类，并对每个CZI类绘制F-对数图。图10显示了F-对数图。

按CZI范围值划分的每组岩石的F-对数图

图11是每个CZI区间或类别的m-图，显示了胶结系数数据与孔隙度值的高度分散。

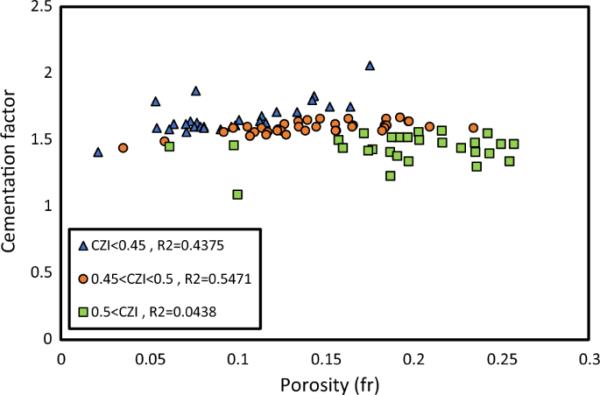
m- plot表示按CZI范围值进行分类的每组岩石

根据地层电阻率因子对孔隙度的对数尺度图(图10)，得到各CZI组的F-方程及m、a、R2值如表6所示。

表7给出了根据胶结系数与孔隙度的交叉图得到的各CZI层段的m-方程和R2(图11)。

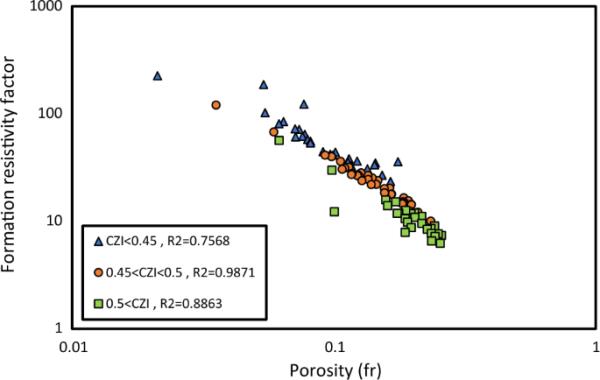
从图10可以看出，在F-对数图上用它们的CZI区间来说明数据，虽然数据有一些波动，R2值不同(分别为0.7568、0.8863和0.9871)，但得出的组几乎是不同的。尽管如此，CZI几乎可以将石灰石划分为不同的组。这是因为CZI的主方程(即式(19))中有一项表示岩石的固体部分(即基体)电阻率最高。因此，CZI不能完全对灰岩进行很好的分类，但考虑到以上几点，它是一种几乎(不完全)准确的岩石分类方法，仍然是a和m值相同的储层分离的有效方法。

为了根据岩石的电效率值对其进行分类，第一步是使用Eq.(22)对每个岩石样本估计数量，然后绘制其概率图。在这方面，彼此最接近的数据被认为属于同一组。然后，应该将从概率图中获得的每个组的F-对数图描绘为一个区间。在图12中，概率图已经证明了电效率或数据的逆。因此，已经确定了5组不同的。图13显示了每组的F-对数交叉图。

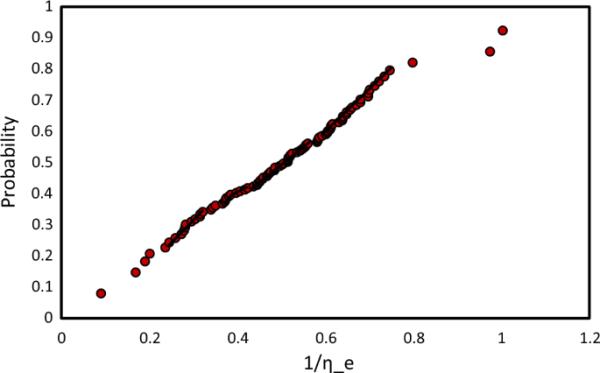
电效率数据逆的概率图

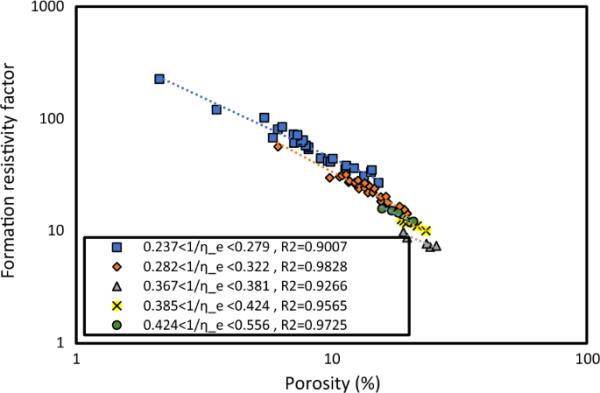
每组岩石的F-对数图，根据它们的逆电效率值进行分类

表8给出了基于地层电阻率系数对孔隙度的对数图的各电效率逆区间的F-方程及m、R2、a的取值(图13)。

如图13和表8所示，每一组都被划分为完全不同的类别。基于得到的R2值较高(分别为0.9007、0.9828、0.9266、0.9565和0.9725)和数据的低散射，我们可以推断电效率是将石灰石划分为不同电类群的精确方法。基于电效率值对岩石进行准确分类的原因是储层岩石是多孔介质，不同孔隙度值的弯曲系数和路径不同。因此，每条路径的电效率都会有所不同。

最后，我们将我们提出的新方法应用于Regnet等人(2015)的数据。在该方法中，根据数据的扭曲系数值对数据进行分类。因此，数据被划分为10个不同的区间。然后，数据在F-对数图上进行了说明，如图14所示。该图显示了每个扭曲系数组或区间的F对数图。

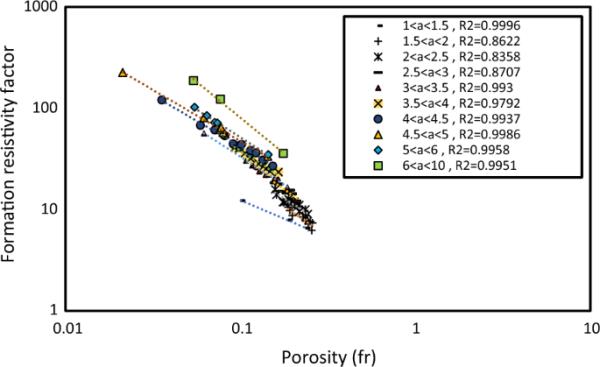
每组岩石的F-对数图，按其弯曲系数范围值进行分类

根据地层电阻率系数对孔隙度的对数图(图14)，得到各弯曲系数区间的F-方程及m、R2、a的取值如表9所示。

从图14中可以看出，每一组扭曲系数都与其他组不同，在数据中都属于一个不同的低散射组，从表9中可以得到R2的高值(分别为0.9996、0.9937、0.9986和0.9951)。数据的低散射意味着基于其扭曲系数值对岩石进行分类是一种准确的岩石分类方法。这是因为挠度系数是指示流体电路径的一个参数，因此，它是石灰石的准确分类方法。

由于胶结系数对某些岩石物性影响很大，因此准确估计胶结系数至关重要。岩石分型是精确测量胶结系数的方法之一。在本研究中，Regnet等人(2015)报告的数据除了使用一种新的岩石分类方法外，还使用了传统的方法进行分析。本研究的结果可以总结为以下几点:

• 基于渗透率和流带指标的岩石分类由于其分析数据的高散射性，不能被认为是准确的岩石分类方法。

• 当前分区指标是一个参数，很少能作为岩石分类的精确方法。

• 电效率数据分析表明，基于电效率的岩石分类方法是一种较为准确的岩石分类方法。

• 基于岩石的扭曲系数值对岩石进行分类是本文提出的一种新的岩石分类方法。这是将岩石划分为不同类别的另一种方法，也可以认为是岩石分类的一种准确方法。利用弯曲系数分类得到的方程对数据进行分析后发现，地层电阻率系数的数值与初始地层电阻率系数数据的数值完全相似。由此可见，该方法是一种准确的岩石分类方法，可以准确预测胶结系数。

下载原文档：https://link.springer.com/content/pdf/10.1007/s13202-023-01659-6.pdf